Input oriented model

The following DEA model is an input-oriented model where the inputs are minimized and the outputs are kept at their current levels.

\[\begin{split}& \theta^* = \min \theta, \text{subject to} \\ & \sum_{j=1}^{n} \lambda_j x_{i, j} \leq \theta x_{i, o}, \quad i=1,2, \dots, m; \\ & \sum_{j=1}^{n} \lambda_j y_{r, j} \geq y_{r, o}, \quad r=1,2, \dots, s; \\ & \sum_{j=1}^{n} \lambda_j = 1 \\ & \lambda_j \geq 0, \quad j=1,2, \dots, n.\end{split}\]

where \(DMU_o\) represents one of the \(n\) DMUs under evaluation, and \(x_{i, o}\) and \(y_{r, o}\) are the \(i\) th input and \(r\) th output for \(DMU_o\), respectively.

Import modules and prepare data.

Sample supply chain data is generated.

import matplotlib.pyplot as plt
import pandas as pd

from Pyfrontier.frontier_model import EnvelopDEA

supply_chain_df = pd.DataFrame(
    {"day": [1, 2, 4, 6, 4], "cost": [5, 2, 1, 1, 4], "profit": [15, 15, 15, 15, 15]}
)
supply_chain_df

	day	cost	profit
0	1	5	15
1	2	2	15
2	4	1	15
3	6	1	15
4	4	4	15

Fit dea model.

The necessity inputs are inputs and outputs. The result has below belongings.

dea = EnvelopDEA("CRS", "in")
dea.fit(
    supply_chain_df[["day", "cost"]].to_numpy(),
    supply_chain_df[["profit"]].to_numpy(),
)

dea.result[0]

EnvelopResult(score=1.0, id=0, dmu=DMU(input=array([1, 5]), output=array([15]), id=0), weights=[1.0, 0.0, 0.0, 0.0, 0.0], x_slack=[-2.5998335e-12, -5e-12], y_slack=[2.3999136e-11], orientation='in')

Visualize the result.

.

eff_dmu = [r.dmu for r in dea.result if r.is_efficient]
ineff_dmu = [r.dmu for r in dea.result if r.is_efficient != 1]
weak_eff_dmu = [r.dmu for r in dea.result if r.has_slack]

plt.figure()
plt.plot(
    [d.input[0] for d in eff_dmu],
    [d.input[1] for d in eff_dmu],
    "-o",
    label="efficient dmu",
)
plt.plot(
    [d.input[0] for d in ineff_dmu],
    [d.input[1] for d in ineff_dmu],
    "o",
    label="not-efficient dmu",
)
plt.plot(
    [d.input[0] for d in weak_eff_dmu],
    [d.input[1] for d in weak_eff_dmu],
    "o",
    label="weak-efficient dmu",
)
plt.plot([4, 6], [1, 1], linestyle="--", color="black")
plt.legend()
plt.show()

About slack

.

print([r.score for r in dea.result])
print([r.is_efficient for r in dea.result])
print([r.has_slack for r in dea.result])

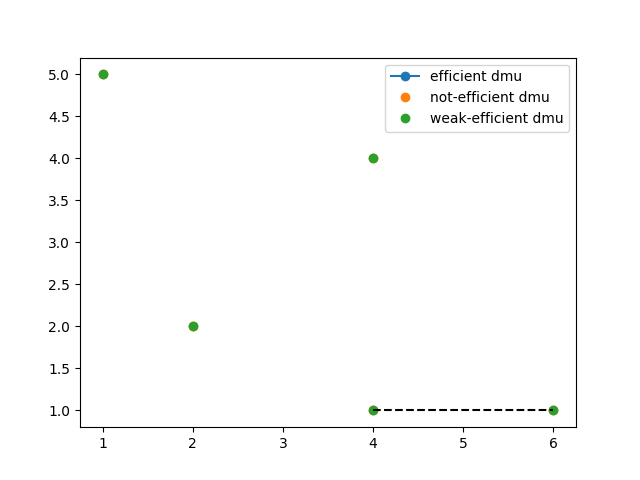
print(dea.result[-2].x_slack, dea.result[-2].y_slack)

[1.0, 1.0, 1.0, 1.0, 0.5]
[False, False, False, False, False]
[True, True, True, True, True]
[2.0, 0.0] [0.0]